摘要:本文首先介绍了磁性材料的特性,然后根据它的特性,讨论电子镇流器中电感线圈参数的选择与计算方法,包括选用磁芯尺寸、气隙大小、线圈圈数和漆包线线径等。
关键词:锰锌铁氧体 初始磁导率 磁通密度 饱和磁通密度 功率损耗 居里温度 气隙
考虑到一些工程技术人员对磁性材料及所涉及的计算公式不够熟悉,为便于展开讨论,本文从基础知识讲起,首先介绍在电子镇流器中常用的锰锌铁氧体磁性材料的一般特性和磁路的基本计算公式,然后,在此基础上,再讨论电感线圈计算中有关问题,包括磁芯尺寸、气隙大小、磁芯中的磁感应强度、磁芯损耗以及线圈的圈数和线径的计算等。这些内容对于从事电子镇流器设计的人员无疑是很有用的。
一.锰锌铁氧体磁性材料的一般特性
表征磁性材料的磁性参数有以下数种:
1.初始磁导率μi
初始磁导率是基本磁化曲线上起始点的磁感应强度B与磁场强度H之比。任何一种磁性材料的初始磁导率可以按以下方法求得:用该材料做成截面积为A(cm2)的圆环,平均直径为D(cm),在圆环上均匀分布绕线N匝,在LCR电桥(例如TH2811C数字LCR电桥)上,测出其电感为L(H),则可按下述计算公式求出其磁导率
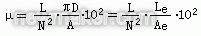
式中,Le、Ae分别代表磁芯磁路的有效长度及有效面积,如式(1)除以真空磁导率μ0(μ0=4π×10-7(H/m)),则得到相对初始磁导率,它可以表示为:

式(1)、(2)中,L的单位为亨(H),D、有效长度Le的单位为cm,A、有效面积Ae的单位为cm2。如D、A分别换用mm、 mm2为单位,则式(2)中最后一项应换成1010。公式(2)由于除以μ0,所以是无量纲的,一般在磁性材料的工厂手册中给出的初始磁导率,就是按式(2)求得的。
例1 有一个R5K材料磁环,其尺寸为外径12mm、内径6mm、厚4mm,试计算其相对初始磁导率。
解:在磁环上绕4匝线圈,测出其电感(用TH2811C数字LCR电桥在10kHz条件下测量电感)为53.1μH。直接查厂家提供的数据表,查得磁环的有效磁路长度Le=26.1mm,有效截面积为11.3mm2。如没有这些数据,作为粗略估算,其有效磁路长度可按外径和内径的平均值计算出圆环的周长来代替,即Le=π(12+6)/2=9π mm=28.2mm;有效截面积并非等于由磁环厚度与其外径、内径之差的乘积计算出的实际面积,而应考虑磁场强度(或磁通密度)沿半径方向内强外弱的线性变化,磁通并非均匀分布,故实际面积应除以2,才是其有效面积。按这样方法求得的值为12mm2,与手册表中所给数据差不多,代入式(2)得:
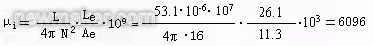
根据以上计算,上述材料应为R5K材料。目前工厂使用的测量磁导率的仪器,如磁环参数分选仪UI9700,仪表指示的不是相对初始磁导率的绝对值,而是它的相对大小。
磁性材料的初始磁导率μi不是固定的,它随温度的变化而变化,如图1所示。图中给出的是金宁公司的磁性材料JP4A(相当于TDK的PC40)的初始磁导率随温度变化的曲线。

图1 (相对)初始磁导率随温度之变化
2. 有效磁导率eμ(Effective permeability)
在闭合磁路中,用有效磁导率μe来表示磁心的导磁性能:
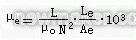
式中,L为装有磁心的线圈的电感量(亨利,H),N为线圈的匝数,le为磁芯的有效磁路长度(mm),Ae为磁芯的有效截面积(mm2)。μ0为真空磁导率(4π×10-7H/m)
显然这里μe是相对于真空磁导率的比值,也是无量纲的。
如果在闭合磁路中,磁芯各段截面积不同,此时磁芯的有效磁导率为
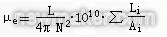
式中 L为装有磁芯线圈的自感量(亨),N为线圈匝数,
Li为具有均匀截面积第i部分的磁路长度(mm)
Ai为该部分的截面积(mm2)
对于一个中心开有气隙长度为lg的E形磁芯,如忽略磁芯本身的磁阻,认为磁场强度全部降落在气隙上,则有效磁路长度即等于lg,式(4)最后一项可去掉Σ符号,简单地写作lg/Ae,如此,式(4)将变为
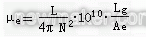
因为空气隙的相对有效磁导率μe为1。以μe=1,带入上式,由此可得气隙lg的表达式为:
lg=4π?10-10N2?Ae/L (5)
式中,lg 以mm为单位,Ae 以 mm2为单位,L以亨为单位。在国外某些公司发表的技术资料中采用式(5)作为初步估算气隙长度的依据。但如果计算出来的气隙不够大,则磁芯部分不能忽略不计,这个数值是不够准确的。
3. 电感因数(Inductance Factor)
电感因数是指磁芯的单匝电感量。一个装有磁心的电感,绕有N匝线圈,其电感值为L,则磁芯的单匝电感量即电感因数AL,可按下式求得:
AL= L/N2 或 L=N2?AL (6)
AL 单位为nH/匝2(有的资料省去分母不写, 简写为nH)。一般取N=100,测得电感量L后,按式(6)计算出AL值,厂家在其产品手册会给出未磨气隙的每种规格磁芯的AL值以及有效磁路长度、有效截面积、有效体积等,例如PC30材料EEI3的AL值为1000nH;EE16A的AL值为1100nH;EE25A的AL值为1900nH。由于磁性材料参数的零散性,这个数值并不很准确,有+/-(15~25)%的误差。我们使用时,一般都磨气隙,由于有气隙存在,AL值虽然变小了,但是电感因子却相对稳定了,零散性也小了。为求得磨气隙后磁芯的AL值,我们可以在相应骨架上先绕100匝,装上磁心,测得其电感值L,根据式(6),即可算出开气隙后磁心的AL值。例如EE25A中心磨气隙1.6mm.后,其AL值降为59.6 nH。
已知某种型号磁芯的AL值,要求绕制的磁芯线圈的电感量为L,可求得所需绕的线圈的匝数N
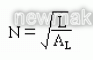
电感量和圈数的平方成正比,圈数变化1%,电感量大约变化2%。在绕制电感时,如只在小范围内改变电感量时,可按此原则调整、估算圈数。
例2 已知EE16(中心磨气隙0.8mm)的AL值为46.8 nH/匝2,为绕制2.8mH的电感,应绕多少匝数N?
解:根据式(7),代入L及值,得
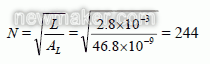
例3 已知某电感采用EE16磁芯,所绕匝数N1为305、电感量L1为4.5mH,今欲绕制的电感为L2=3.4mH,试求出应绕的匝数N2
解:由公式(7)知

两式相除,得

代入相应值
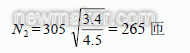
所以,已知磁芯的AL值,对于确定电感所应绕的匝数是很有用的。
4.饱和磁通密度(Saturation magnetic flux density)
饱和磁通密度是一个很重要的参数,对镇流器是否能可靠地工作关系很大。如所熟知,当电流(或磁场)增加到某一数值后,磁芯就会饱和,磁通密度不再增加,如图2的曲线所表示的那样。此时,磁导率很低,该磁通密度称为饱和磁通密度,以Bs表示之。Bs不是固定的,随温度的升高而下降,在80~100°C下,比室温下低得很多。由图2可以查出,在节能灯中常用的PC30、PC40材料在25℃时,Bs=510mT,而在100℃时,Bs只有390 mT,下降了20%多。应该指出的是,磁芯工作时允许的磁感应强度要比上述的390 mT低得多,一方面因为在100℃时接近300 mT附近磁芯的磁导率已开始降低,另一方面,如工作时磁芯的磁感应强度较大,则磁芯损耗亦较大(见图4)。所以在工程计算中均取B为200~230mT作为磁芯工作时允许的最大磁感应强度值,远离磁饱和。
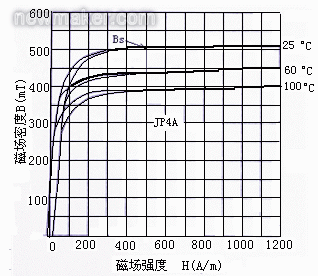
图2 饱和磁通密度随温度变化曲线
在一体化节能灯或电子镇流器中所用磁性材料,如果由于工作温度升高,则其磁芯的Bs值下降,造成磁导率及电感量减少,流过电感的电流上升,在电流的峰值附近出现很大的尖峰,如图3所示。这种情形是很危险的,它会导致电感量进一步减少及电流进一步加大,最终使电感失磁,L=0,三极管因电流过大、管子结温过高而损坏。
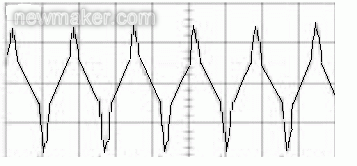
图3 电感饱和后电感线圈中的电流波形
5. 磁性材料的功率损耗(Power loss of magnetic material)
磁性材料的功率损耗是一个很重要的参数,它反映磁芯工作时发热的程度,损耗大,发热就厉害。带有磁芯的线圈,其功率损耗包括线圈电阻的功率损耗(俗称铜耗)和磁芯材料的功率损耗(俗称铁耗)。磁芯材料的功率损耗包括磁滞损耗、涡流损耗和剩余损耗三部分。
大家知道,磁芯中磁感应强度B的变化滞后于磁场强度H的变化,并呈现出封闭的磁滞回线形状,磁滞损耗的大小与磁滞回线所包围的面积呈正比。也与频率成正比。
涡流损耗则是由于交变磁通穿过磁芯截面时,在与磁力线相垂直的截面内环绕交变磁通会产生涡流,涡流亦产生功率损耗。它与磁通变化的频率,磁性材料的电阻大小有关。一般磁芯材料的电阻愈大、工作频率愈低,涡流损耗愈小;反之亦然。
上述损耗与频率及其工作时的磁感应强度有关,工作频率愈高、磁感应强度愈大,则其损耗亦愈大。
图4给出了磁性材料JP4A(PC40)在不同的磁感应强度下损耗随频率变化的情况,随着频率增加,损耗亦加大。例如在200mT、100oC的工作条件下,当频率由20kHZ变为40kHZ时,功率损耗密度由20kW/m3(20μW/mm3)增加为50kW/m3(50μW/mm3),大约增加为原来的2.5倍。可见,在同样的磁感应强度下,磁心损耗随其工作频率的增加而增加。因此,提高镇流器的工作频率,则电感损耗将加大;反过来,降低镇流器的工作频率,将有利于减少镇流电感的功耗和发热。在某些大功率的镇流器中,把频率调到20~30kHZ附近,其目的即在于此。
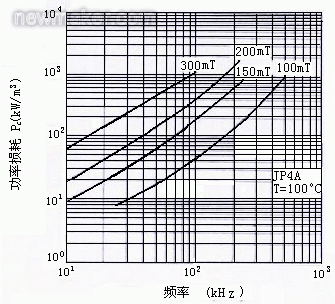
图4 在不同的感磁应强度下损耗随频率的变化
由图还知,在同一频率下,磁芯损耗随磁感应强度的增加而增加,例如在40kHZ、100°C条件下,当磁感应强度由150mT增加到200mT时,功率损耗密度由50kW/m3增加为100kW/m3,大约增加为原来的2倍,如果磁感应强度为300mT时,功率损耗密度将增加为250kW/m3,大约增加为原来的5倍。
可见,磁心损耗随其工作感磁感应强度的增加而增加。同一种材料和尺寸的磁心,在保持电感不变时,增加气隙,能减少其磁感应强度(以后会讲到),对于降低功率损耗是有利的。或者,在同样的气隙下,减少电感量,就会减少磁感应强度,也能降低磁芯的损耗。当然,如采用大一号的磁心,也会大大降低磁心的磁感应强度和它的发热程度。不过,增加气隙,虽能减少磁芯损耗,但线圈的圈数要增加,铜损会增大,而且窗口的面积会容纳不下线圈。所以,气隙的增加也是有限度的,并非愈大愈好。应对铜损和铁损两者综合加以考虑才对。
例4 已知某大功率电子镇流器所用电感为PC40(JP4A)材料、EE28磁芯,磁芯的磁感应强度为200mT,EE28的有效体积Ve为5254mm3。计算它在100°C的条件下,当频率为20kHZ和40kHZ时磁芯的功率损耗,如磁感应强度增为300mT,再计算其损耗。
解:磁芯的损耗P=PC×Ve,在图4中查出相应的单位体积的损耗PC值
当磁感应强度为200mT时,在20kHZ时,P=20μW/mm3×5254mm3=0.105W
在40kHZ时,P=50μW/mm3×5254mm3=0.26W
当磁感应强度为300mT时,在20kHZ时,P=105μW/mm3×5254mm3=0.55W
在40kHZ时,P=350μW/mm3×5254mm3=1.8W
可见,在100°C、300mT时,磁心的损耗是十分惊人的,所以,降低工作频率和磁感应强度很有必要。选择磁芯工作的磁感应强度,不仅从是否饱和,还要从损耗大小综合考虑,前面提到的以200~230mT作为计算磁感应强度B的参考值,就是基于以上的双重考虑。
图5表示JP3(PC30)、JP4A(PC40)在不同的频率下损耗随温度变化的情况。材料的损耗在某一温度下为最低,出现一个谷点。在谷点左边,随温度的增加,损耗减少;在谷点右边,随温度的增加,损耗亦增加。
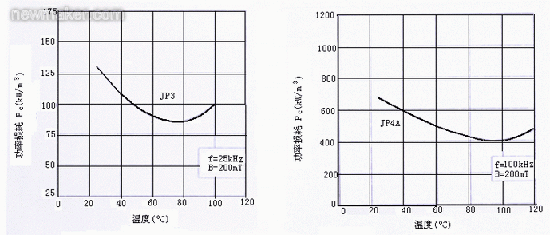 图5 磁芯中功率损耗随温度的变化曲线
图5 磁芯中功率损耗随温度的变化曲线
对于PC30(JP3)材料,谷点大约在75℃左右,对于PC40(JP4A)材料,谷点大约在90~95℃左右。我们希望磁性材料稳定的工作温度处于损耗曲线的谷点温度附近。也就是说,如能保持PC30电感磁心的温度为75℃左右,而PC40电感磁心的温度在80~90℃左右,或者稍低一些,那么,电感损耗将为最低,或者随温度的上升而有所下降,电子镇流器的可靠性将最高。可见PC40(JP4A)材料适合在较高的温度下工作,而PC30材料适合在较低的温度下工作。
磁性材料还有其它的参数如居里温度、功率损耗密度…等,一般对它的理解都很清楚,不再赘述。
二.磁感应强度的计算公式
由交流电路基础知,在有磁心线圈的均匀磁路中,如线圈的圈数为N,电感为L,流过线圈的电流为i,则线圈两端的电压u有:
u=Ldi/dt=Ndφ/dt, 或写作: u= LΔi/Δt=NΔφ/Δt,
从而得 LΔi=NΔφ,
如电流是交变的正弦波,则可按符号法分析,电流和磁通以有效值表示,则有:
NΦ=LI, (9)
又知电感量 L与圈数N的关系为: L= AL×N2
代入式(9),求出磁心中的磁通Φ为:
Φ=LI/N=N2×AL×I/N=N×AL×I
考虑Φ=B×Ae,由此可得,磁心中的磁感应强度B与流过线圈的电流I和线圈圈数N之间的关系为:
B=Φ/Ae=N×AL×I/Ae (10)
上式中,B的单位为T(特斯拉)、I的单位为安、Ae的单位为m2、AL的单位为亨/匝2。
式(10)是一个很有用的公式,根据它,可以对已绕制的电感线圈计算磁芯的磁感应强度,以判断磁芯会不会饱和,工作是否可靠。
或者,根据已知的(允许的)磁感应强度B,可由式(10)求出在一定的线圈工作电流I下,允许绕制的最大圈数N,得:
N=LI/φ=LI/B×Ae
已知电感量L和规定的磁感应强度B,则线圈的圈数和磁芯的有效面积Ae的乘积必须满足:
N×Ae=LI/B (11)
国外有的公司提供的磁芯数据表中会给出磁芯尺寸和在一定线径下的 N×Ae值。由式(11)就可以选用合适的磁芯尺寸和线圈的线径了。在国外公司提供的应用指南中就有这样的计算实例。我国的磁性材料厂家一般都不提供这样的资料,所以按式(11)来选用磁芯不太现实。
三。磁芯气隙对磁感应强度的影响
磁芯气隙对磁感应强度的影响是一个很重要的问题,如何选择气隙,至关重要,我们不妨通过一个具体例子来作进一步的说明。
例5 已知在一拖二36W电子镇流器中,要求的电感量为2.1mH,根据在工作台上测试,流过此电感的电流(有效值)为0.3A,试选用磁芯,并计算磁心的有效磁导率、磁芯中的磁感应强度B,如果不加气隙,有没有饱和的问题?如果磨气隙1.6mm,情况怎样?
解:首先根据经验以及电子镇流器的功率大小,我们初步选用EE25 磁芯,由厂家的数据表查出:它的有效截面积Ae为39.6mm2,电感因子AL=1900nH,有效磁路长度为49.5mm。
(1)如果不加气隙,根据其厂家提供的电感因子AL数据,要绕制2.1mH的电感,其圈数为:
N=(2.1×10-3/1900×10-9)1/2=33圈,
(2)按式(2),未磨气隙的磁芯的有效磁导率为
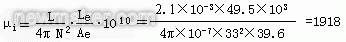
其磁导率为2k,说明这是R2k或R2.5k材料。对于磨有气隙的磁芯不能用式(3)计算磁导率,因为磁芯不是均匀的。
(3)磁感应强度
根据电感量、圈数、及流过线圈的电流,按式(10)求得:
B=N×AL×I/Ae =35×1900×10-9×0.3/39.6×10-6=0.503T=503mT
这样大的磁感应强度,即便在室温下磁芯肯定要饱和。如果再考虑到磁性材料参数的不一致性,有+30%的误差,以及灯电流波峰系数(一般限制为1.7以下,有时可能更大),则在电流最大的峰值(1.7×0.3=0.51A)附近,磁感应强度最大值将达到
BM=1.7×503mT=855mT,
再加上AL值+30%的误差,磁心的磁感应强度更是大得不得了,磁芯肯定饱和。 饱和时,磁心中的电流波形将如图3所示。
所以,不磨气隙,或气隙太小,电路是不可能正常工作的。
(4)如果在中心磨气隙1.6mm,其电感因子经测试降为AL=59.6nH,电感因子降低了1900/59.6=31.9倍。为绕制2.1mH的电感,其圈数变为
N=(2.1×10-3/59.6×10-9)1/2=188圈,
由于电感与圈数的平方成正比,线圈圈数N只增加了188/33=5.7倍。这样,电感因子大幅度减少,而圈数增加并不多,所以磁感应强度下降了。
在磨气隙后,按式(10),磁感应强度B变为:
B=N×AL×I/Ae =188×59.6×10-9×0.3/39.6×10-6=0.084T=85mT
可见,磨气隙后,磁心的磁感应强度大幅度下降。气隙越大,磁芯的磁感应强度越低,电感线圈越不容易饱和、损耗越小,越可靠,但是用的漆包线变多了。
在85mT的磁感应强度下,即便考虑电流的波峰系数=1.7,最大的磁感应强度也不过144.5mT(加气隙后,AL值是稳定的,没有误差),那怕温度上升,磁芯也肯定不会饱和。
这个例子充分说明:如果没有气隙,在上述电流下,由于磁场强度太大,磁心会饱和。所以作为镇流器的扼流电感,磁心必须加足够大的气隙,减少其有效磁导率,用增加圈数的办法来得到所希望的电感量。因为磨气隙,电感因子AL会减少很多,但电感量是与圈数N的平方成正比,圈数增加并不多,所以磁芯的磁感应强度会大大下降,就不会饱和了。
磨气隙后,材料的有效磁导率μe和电感因子之所以会降低,是因为磁路的磁阻变大了,相当于有效长度Le加长了。由理论知,磨气隙后,存在以下关系式:
H=NI/Le
B=μeH (12)
tgδ(gap) = tgδ×(μe/μi)
以上三式表明,磁场强度H和有效磁导率μe下降,磁感应强度B亦随之下降。
在同样的电感和同样的电流下,增加气隙后,磁场强度H减少,再考虑有效磁导率μe减少,结果,带来的第一个好处是:磁感应强度(磁通密度)B必然大幅度下降,磁心就不会饱和了。式(12)中 tgδ(gap) 为有气隙的损耗角正切(或损耗因子),它表示磁心的损耗。此值愈大,损耗愈大。由于μe<μi,所以增加气隙后,损耗因子减少,带来的第二个好处是磁心的损耗减少了。
经验证明:磨气隙后,还会增加磁性材料参数的的稳定性和一致性,减少磁心尺寸参数离散性的影响,带来的第三个好处是使绕制的电感一致性变好。
这里提醒一下,如果电感是外加工的,一般加工方为了节省铜材,都愿采用较小的气隙,这样做,对于镇流器来说是很危险的。因此在给外加工的加工规范中,必须对气隙做出明确而严格的规定。如果是自己绕制电感,在选用好磁心、气隙和圈数后,不要忘了按式(10)计算一下磁心的磁感应强度,判断电感在最高工作温度和最大电流下有没有饱和的可能,并留有一定的余地。
一般在已知线圈通过电流(有效值)的条件下,计算出来的磁感应强度应在200~230mT以下为宜,不能太大。如果计算出来的值达到300mT以上,磁芯不仅可能饱和,而且损耗过大,这是不能允许的。这时应加大气隙,或选用大一号的磁芯。
一般来说,磁芯尺寸愈大,气隙亦应愈大。作为经验值,我们推荐:EE13的中心气隙应≥0.4mm,EE16的中心气隙应≥0.6mm,EE19的中心气隙应≥0.8mm,EE25的中心气隙应≥1.3~1.5mm,EE28的中心气隙应≥1.5~1.8mm,EE30的中心气隙应≥1.8~2.0mm等等。为了给气隙的选择找到一个合理的而不是盲目的依据,建议对每种规格的磁心,磨不同的气隙,计算它在不同的电流和电感量下的磁感应强度,根据磁感应强度值,来判断气隙大小是否合适。
例6 通常用磁心EE16A(A×B×C=16×7×5)来做25W以下节能灯的电感,采用0.5 ~0.8mm的气隙,磁心的有效面积为18.4mm2,,已知灯的实测参数如下:
(1)3U15W灯:电感为4.2mH,导入阴极电流为148mA,灯功率为13.5W,电流波峰系数CCF=1.6
3U24W灯:电感为2.4mH,导入阴极电流为217mA,灯功率为22.4W,电流波峰系数CCF=1.63
试分别计算其磁感应强度,判断磁心是否会饱和?在同样的电感量下,允许流过线圈的最大电流是多少?
(2)如果磁芯的气隙为:0.5mm,磁心的电感因子为63.5nH/匝2,情况又将如何?
(3)如果设计不好,例如磁环圈数太多,驱动过分,24W的灯要求电感量为3.5mH,其它情况不变,即导入阴极电流仍为217mA,灯功率为22.4W,电流波峰系数CCF=1.6,此时情况又如何?
解:
1。气隙为0.8mm时,由例2知,磁心的电感因子为46.8nH/匝
对于15W的灯:
(1)为得到4.2mH电感,应当绕的圈数为
N=(4.2×10-3/46.8×10-9)1/2= 299圈
(2)按式(10),磁感应强度为:
B=N×AL×I/Ae=299×46.8×10-9×0.148/18.4×10-6=112mT,
即便考虑电流波峰系数为1.6,最大磁感应强度 BM为:
BM=N×AL×IM/Ae=112mT×1.6=179mT
磁心也不会饱和。
(3)如果允许最大磁感应强度BM为200~230 mT,则允许流过的最大电流为
IM=BM×Ae/N×AL=(200 ~230)×0.148/112=0.264 ~0.304 A
考虑到电流波峰系数1.6,则允许流过的最大的电流有效值为(0.264 ~0.304)A/1.6=0.165~0.190A。由于实际流过的电流为0.148A,仍有110 ~130%的富裕量,所以对15W灯来说,EE16磁心的富裕量是足够的.
对24W的灯,计算方法同上。
(1)为得到2.4mH电感, 线圈的圈数为
N=(2.4×10-3/46.8×10-9)1/2= 226
(2)磁心的磁感应强度B为
B=N×AL×I/Ae=226×46.8×10-9×0.217/18.4×10-6=125mT
最大的磁感应强度BM
BM=N×AL×IM/Ae=125mT×1.53=191mT
(3)如果允许最大磁感应强度为200 ~230 mT则允许流过的最大电流为
IM= BM×Ae/N×AL=(200 ~230)×0.217/125=0.347 ~0.399 A。考虑到电流波峰系数1.63,最大的电流有效值为(0.347 ~0.399 )A )/1.63=0.212 ~0.245 A。与实际的电流有效值0.217A相比,基本上没有什么富裕量了。
2。气隙为0.5mm时,磁心的电感因子为63.5nH/匝2
对于15W的灯:
(1)为得到4.2mH电感,应当绕的圈数为
N=(4.2×10-3/63.5×10-9)1/2= 257圈
(2)按式(10),磁感应强度为:
B=N×AL×I/Ae=257×63.5×10-9×0.148/18.4×10-6=131mT。
与0.8气隙相比,减少气隙,线圈圈数减少了,但磁芯中磁感应强度变大了,这时磁芯中损耗也会增加。
本例中,对15W的灯,如气隙为0.5mm即便考虑电流波峰系数为1.6,最大磁感应强度 BM也不过为:
BM=N×AL×IM/Ae=131mT×1.6=210mT
磁心不会饱和,还是有一些富裕量。
对24W的灯
(1)为得到2.4mH电感, 线圈的圈数为
N=(2.4×10-3/63.5×10-9)1/2= 194
(2)磁心的磁感应强度B为
B=N×AL×I/Ae=194×63.5×10-9×0.217/18.4×10-6=145mT,
考虑电流波峰系数为1.6,最大磁感应强度 BM为:
BM=N×AL×IM/Ae=145mT×1.6=232mT
磁心虽不会饱和,但已接近允许最大磁感应强度BM。所以,对于24W功率的灯,还是用0.8mm气隙为好。
由以上计算表明,对15W的灯,由于电流及功率较小,EE16磁芯采用0.5 mm的气隙是可以的、合适的;对于24W的灯,由于电流较大,建议采用0.8 mm的气隙。
3。如24W灯要求电感量为3.5mH,流过电感的电流仍为217mA, 此时为得到所需要的电感量,线圈的圈数为:
N=(3.5×10-3/63.5×10-9)1/2= 235
磁心的磁感应强度变为:
B=235×63.5×10-9×0.217/18.4×10-6=175mT
考虑电流波峰系数为1.6,最大磁感应强度 BM为:
BM=N×AL×IM/Ae=175mT×1.6=280mT
这种情况下,磁芯中的磁感应强度超过了所推荐的200 ~230 mT。极容易变为饱和,且损耗增大,电路变得不可靠了。
由此看来,在磁芯尺寸一定的条件下,电感量越大,气隙越小,磁芯中磁感应强度越大,在同样的电流下,越容易造成电感饱和。而且,磁芯中的损耗也随磁感应强度变大而增加,发热也越来越严重,电路越不可靠。
四.线圈中电流之计算及线径的选择
为了合理选择漆包线的线径,必须知道流过电感的电流。在图6(a)的单启动电容的电路中,流过电感的电流,等于导入阴极电流(它等于灯管电流与灯丝电流之向量和,即其平方之和的根值),一般可由仪器测得。在双启动电容图6(b)中,仪器所测的导入阴极电流,已不正确,比实际流过电感的电流少,应加以修正。考虑到辅助启动电容C2并在灯管两端,与启动电容C1上的高频电压差不多相等,流过C2的电流与流过C1的灯丝电流同相,且大小与其容量成正比,因此可用电流IF'=(1+C2/C1)IF,代替原来的灯丝电流,然后根据修正后的这一电流,求出它与灯管电流的向量和,即它的平方值与灯管电流的平方值之和,再求出其根值,就可以得到真正流过电感的电流了。
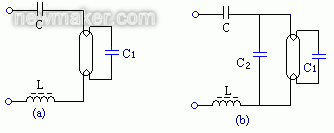
图6 流过电感的电流
例7 某55W电子镇流器,实际输入功率为40.2W,采用单启动电容8n2,用电感L=2.3mH,由电子镇流器综合测试仪测得的灯管电流为0.322A,灯丝电流为0.157A,导入阴极电流为0.361A,试计算其电感线圈的圈数和线径。
解:考虑其电流较大,这里选用EE25A磁心(25×10×6,中心磨气隙1.5mm。用100匝的线圈去测得该磁心的电感为596μH,由此可以算出其AL值为596/1002=59.6nH/匝2
1)线圈的圈数
为绕制2.3mH的电感,按公式(7),线圈的圈数
N=(L/AL)1/2=(2.3×106/59.6)1/2=196匝
2)线圈的线径
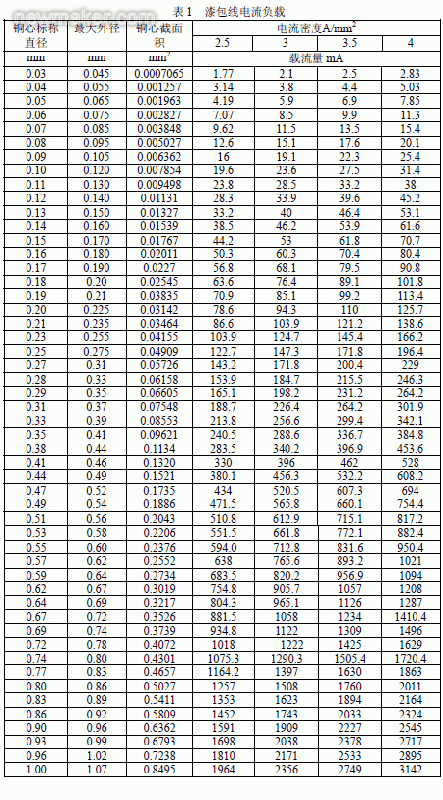
表1 为漆包线的标称直径、铜心截面积以及其载流量等。一般导线的电流密度按2.5A~4A来选取,由表1知,为通过0.361A的电流,导线的载流截面积应为0.08~0.10mm2,可以选用φ0.31或φ0.33的漆包线,其载流截面积分别为0.076、0.0855mm2。计算线圈占用空间时,应考虑漆层厚度,根据表1的最大外径,其实际占用面积分别为0.108、0.119mm2。为经济计,这里选用φ0.31的线,其实际面积为0.108mm2。
3)线圈是否绕得下?窗口是否够?
用一股φ0.31的线,线圈占用的面积为196×1×0.108=21.2 mm2。EE25的窗口面积为42mm2左右,完全绕得下。经试绕后,磁心窗口确实尚有较大的空隙。
4)计算磁芯的最大磁感应强度B
按公式(10),磁芯的磁感应强度B=N×AL×I/Ae
这里I应按最大电流考虑,即它的有效值再乘以电流波峰系数1.7,Ae为磁芯的有效截面积,对EE25A 为39.6mm2,得磁芯的最大磁感应强度:
BM=196×59.6×10-9×0.322×1.7/39。6×10-6=0.161T=161mT,
比一般推荐的磁感应强度200~230mT值低。工作时,不会有饱和问题,损耗也不会太大。根据磁感应强度值可以判断,我们选择气隙的大小基本上是合适的。
装入整灯实际使用后,电感线圈及磁心的温度都不高,可见,磁心尺寸及漆包线线径的选择是合适的。
例8 某75W电子镇流器,实际输入功率为56.7W,采用双启动电容,有灯丝电流的电容C1=4n7,辅助启动电容C2=6n8,电感L=2.6mH。
由镇流器综合测试仪测得的灯管电流值为0.322A,灯丝电流为0.157A,导入阴极电流为0.361A,试计算其电感。
解:考虑其电流更大一些,这里选用EE28磁心,中心磨气隙1.8mm。
为了求得线圈的圈数,必须知道磁心的AL值。为此,可用100匝的线圈去测得磁心的电感为850μH,由此可以算出其AL值为850/1002=85.0nH/匝2。
1)线圈的圈数
为绕制2.6mH的电感,线圈的圈数N=(L/AL)1/2=(2.6×106/85.0)1/2=168匝。
2)线圈的线径
由于采用双启动电容,仪器所测得的导入阴极电流已不是真正流过线圈的电流,必须加以修正。修正后与灯管并联的容性电流=(1+C2/C1)0.157A=(1+6.8/4.7)0.157A=0.424A,由此可算出流过线圈的电流为修正后的容性电流与灯管电流的向量和,即
(0.3222+0.4242)1/2=0.532A.
由表1知,为通过0.532A的电流,导线的载流截面积应为0.16mm2,可以选用φ0.45的漆包线,考虑到趋肤效应,这里选用φ0.29的线双股并绕,其有效线径为1.414×φ0.29=0.41mm,考虑漆包层,其单股实际截面积为0.096mm2。。如嫌线稍细一些,可选用φ0.31的线双股并绕更好。
3)所占用窗口的空间
168×2×0.096=32.3mm2,窗口空间足够。经试绕后,磁心窗口确实尚有一定空隙。
4)计算磁芯的最大磁感应强度BM
磁芯的磁感应强度BM=N×AL×I/Ae=
168×85.0×10-9×0.532×1.7/71.6×10-6=0.180T=180mT
低于推荐值200mT,不会有饱和问题。经试绕后,装入整灯实际使用后,电感线圈及磁芯的温度也都不高,可见,上述磁芯尺寸、气隙大小及漆包线线径的选择是合适的。
在计算漆包线的的电流密度和线的载流截面积时,可按其标称值计算。供应商提供的漆包线规格,均是线材的裸径,不包含漆膜厚度,勿须考虑再减去漆包线的绝缘厚度。一般漆膜的厚度在0.01~0.04mm左右,线径细的,绝缘厚度小一些,而线径粗的,绝缘厚度大一些。在计算线圈占用窗口面积时,应考虑加漆包线漆层厚度后,比漆包线标称值要大,在表1中给出了漆包线最大外径,可按此值,计算其实际截面积,以免磁心的窗口装不下。
例9。计算某有源功率因数校正器的升压电感,电路的输入电压范围为180-265V,直流输出电压为400V,最大输出功率为80W,变换器的效率η为0.95。
根据文献1第七章公式(7-11)知,升压电感L的计算公式为:
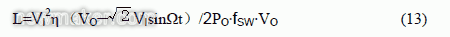
上式中取最低的开关频率为fsw=30kHZ(开关频率一般应不低于23kHZ),在最大的输入线电压VIMAX=265V,且sinΩt=1时,计算电感,并将已知数据代入式(13),得
L=2652×0.95(400─1.414×265)/(2×80×30×103×400)=0.86mH
再在最小的输入线电压VIMIN=180V,且sinΩt=1时,计算电感,并将已知数据代入式(13),得
L=1802×0.95(400─1.414×180)/(2×80×30×103×400)=2.48mH
计算出电感后,取两者之中的小者作为电感值,本例中取L=0.86mH。
为制作电感,L=0.86mH,可选用EE28磁芯,中心磨气隙1.8mm,由例8知其AL值为85.0nH/匝2。要得到0.86mH的电感,线圈的圈数应为:
N=(L/AL)1/2=(0.86×106/85.0)1/2=101匝。
根据第七章的讨论知,流过电感的电流的最大值,等于输入电流峰值的2倍,输入电流在输入电压最低时最大
ILP=2√2II=2√2PI/VI=2√2P0/η I
以 VI=VIMIN = 180V,η为 0.95,P0=80W 代入上式,得ILP=1.32A 。
已知EE28的AL值为85.0nH/匝2,有效截面积87.0 mm2, 则由式(10)得:
B=N×AL×I/Ae
而磁芯中最大的磁感应强度为:
BM= 101 ×85×10-9×1.32/87×10-6=130 mT
可见选用EE28是没有问题的。由于富裕量较大,可以选用更小的气隙,以减少圈数。甚至可以考虑选用更小一号的磁芯,但线圈一定能装得下。
关于线圈线径的选择,同前述方法是一样的。流过电感电流的有效值根据文献1为:
IL=2II/√3 =2P0/(ηVI √ )=2×80/(0.95×180×1.732)=0.54A (14)
按表1,可选用 0.41 ~0.44mm的线。为减少趋肤效应的影响,可用两股φ0.29mm的线或φ0.31mm的线并绕。最后计算线的实际外径,看窗口是否绕得下,升压电感的计算就算完成。
文献1:陈传虞编著 电子节能灯与电子镇流器的原理和制造第一版,北京:邮电出版社。2004年

