摘要:为了解决目前L ED 摩托车信号灯光效低、成本高的问题,提出了一种基于L ED 光强分布数学模型的新方法。在推导了曲面L ED 阵列光强分布数学模型的基础上,将其应用于L ED 摩托车信号灯配光设计。进一步采用Tra2cepro 光学仿真软件对该方法设计的L ED 摩托车制动灯进行了模拟实验,结果证明曲面L ED 阵列光强分布的数学模型正确,能够满足国家摩托车配光标准的要求,从而对实现了L ED 摩托车信号灯的配光设计。
0 引 言
目前通用的摩托车制动灯光源仍然是白炽灯占主导地位,加上红色的配光透镜实现配光要求,其缺点是白炽灯易损坏,功耗大,寿命短,可靠性差,给道路交通带来安全隐患等。LED(发光二极管) 具备体积小、寿命长、低能耗等优势被逐步应用于机动车车灯光源。目前通用的L ED 摩托车信号灯的配光设计方案主要有三种:第一种是直接将多个食人鱼型L ED 排布成平面状密封在灯罩内,其缺点是相当一部分光处在国标配光屏幕要求的范围外,造成光能的浪费;第二种是采用多个球帽型L ED 排布成平面状密封于灯罩内再加上配光透镜配光,其缺点是一部分光经配光透镜折射、散射和吸收,造成灯具光效比较低;第三种是将多个食人鱼型L ED 排布成平面,经抛物型聚光器和配光透镜联合配光。其缺点是聚光器设计成本高,配光透镜光能损失较大。三种配光设计方案设计的LED 摩托车信号灯光效低,光能损失大,设计成本高。
如果能够从理论上建立L ED 光强分布的数学模型,研究一种L ED 阵列的光强分布且无需聚光器和配光镜,使其满足国家标准,从而为L ED 摩托车信号灯设计提供一种新的快捷、实用的方法,具有重要的理论与实际指导意义。
1 曲面LED 阵列的光强分布的数学模型
1. 1 单个LED 光强分布的数学模型
首先建立单个L ED 光强的分布模型,如图1 所示。其中,探测球面中心为(0 ,0 ,0) ,半径为r ,α表示L ED 光源的水平方向角;β表示L ED 光源的垂直方向角;θ表示单个L ED 光线OM 与光轴OL 的夹角;φ表示L ED 光轴OL 与其在x y 平面投影的夹角;γ表示L ED 光轴OL 在x y 平面投影与Y 轴的夹角。
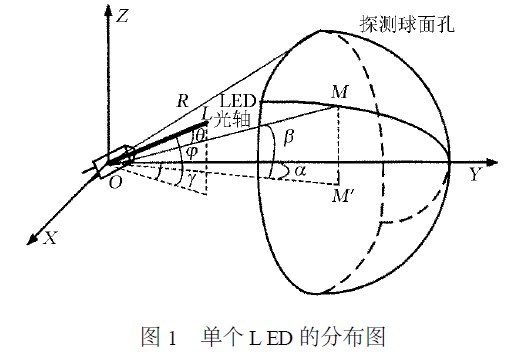
单个LED的分布图
则L ED 光轴对应的单位坐标为(co sφsinγ,cosφsinγ,sinφ) ,探测球面上M点的坐标( rcosβsinα,rcosβcosα, rsinβ) 。
由此,L ED 光源的光强分布可以表示为I =I (θ) 或者I = I (α,β) 。
而单个L ED 的光强分布不是理想的朗伯体,该分布可以表述为:
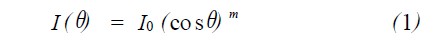
当θ =θ1/ 2 时
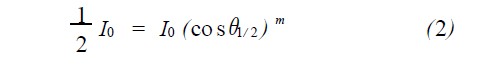
即

由图1 可知,θ也可以表示为L ED 光轴对应的向量OL 与向量OM 的夹角,则
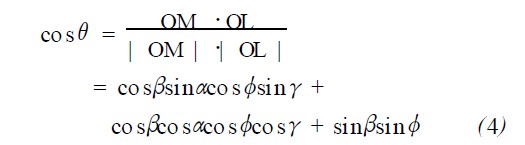
则
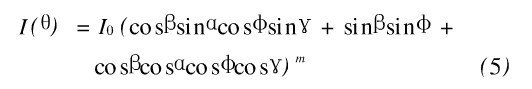
由公式(5) 可知,单个L ED 的光强分布与L ED在空间的倾斜角的垂直分量角φ和水平分量角γ有关,改变φ和γ就可以改变单个L ED 光强的分布。
但是,由于单灯光强小,达不到摩托车信号灯的光强的国标要求,往往需要多个L ED 组合,而改变单个L ED 的倾斜角可以改变光强分布,因此可以进一步研究一种L ED 的曲面阵列排布的光强分布,进而用它来完成对L ED 摩托车信号灯的配光设计。
1. 2 曲面LED 阵列的光强分布的数学模型
当接受屏距离足够远时,多个L ED 组合形成的面光源可以简化为点光源,且相邻两个LED 之间的间距对曲面L ED 阵列的光强空间的影响可以忽略。则曲面L ED 阵列的光强分布只与L ED 的型号、L ED 的个数、以及单个L ED 倾斜角的垂直分量角φ和水平分量角γ有关。
则光强函数表达式可以表述为:
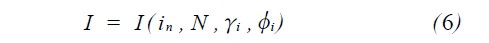
式中I 为LED 阵列的光强; in 为第n 种型号的单个LED 光源; N 为LED 光源的个数。
根据公式(5) 则:
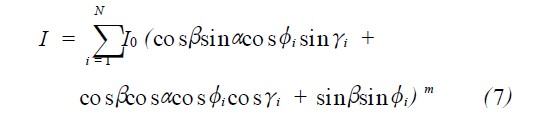
由公式(7) 可知:改变γi 和φi , 可以改变曲面L ED 阵列的分布,通过合理的配置,无需附加反光杯或透镜就可以实现L ED 摩托车信号灯的配光设计。
下面就以L ED 摩托车信号灯为例,介绍该方法的应用。
2 曲面LED阵列的光强分布数学模型在LED 摩托车信号灯配光设计中的应用
2. 1 摩托车信号灯的国家标准
我国摩托车信号灯采用的标准是《摩托车光信号装置配光性能GB T17510 - 1998》,这个标准是针对传统白炽灯的规定,L ED 摩托车灯具的设计也只能继续沿用上述标准, 对于LED 摩托车信号灯的配光性能具体规定如下:
在满足光度学二次平方反比定律距离确定的配光屏幕上,分布在范围为左右20°,上下10°的椭圆形区域内的测试点,光强要求在一定的范围之内,且满足如图2 中的分布。
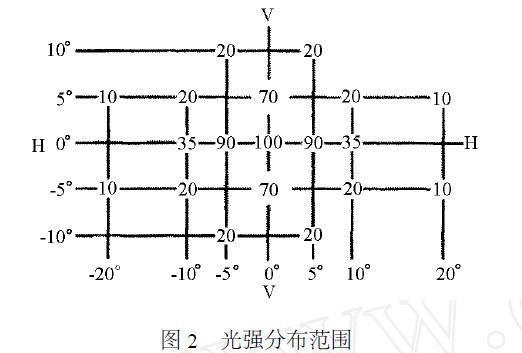
光强分布范围
其中图中的栅格线交叉处的数字为百分比,它表示该方向光强最小值与基准轴线方向光强度最小值的比值,栅格线围成的范围内任一方向测得的光强不得小于该方向周围诸方向中最小的光强值。
2. 2 LED 摩托车信号灯的配光设计
由于单个L ED 的光强达不到国家标准对机动车灯光强的要求,因此采用L ED 的摩托车信号灯必须对L ED 进行阵列排布。
目前,市面上不同型号的球帽型L ED 光源的光强分布范围和国标要求的测点的光强百分比比值不满足图2 所示的国标的光强要求,大部分球帽型L ED 光源的光强集中在水平角和垂直角±15°的范围内且垂直方向的光强分布基本上满足国标光强分布图V2V 方向的分布要求,但水平方向±20°处的光强值几乎为零,因此只需要将水平角15°从扩散到20°,根据公式(7) ,令
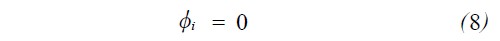
则

根据国家《摩托车光信号装置配光性能GB T17510 - 1998》中摩托车信号灯光强满足的要求,考虑到国标要求光强分布分别关于H - H 对称和V2V 对称,则: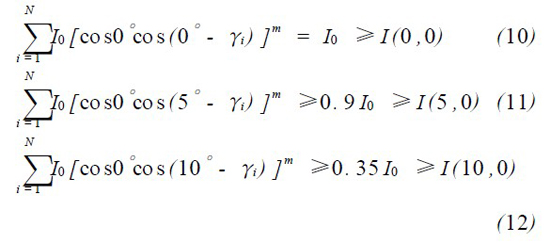

其中I (0 ,0) 表示水平方向角0°,垂直方向角0°时的光强值,其余的类推。
上述方程组若γi 为方程的解,则- γi 亦为方程组的解。考虑实际加工灯具的方便, 假设γi 为等差数列。只需从方程(10) —(18) 中求解出一组满意解γi , 即可以将水平方向的发散角扩散到20°,从而实现对摩托车信号灯的配光设计。
针对摩托车信号灯中具体的一款L ED 制动灯,用上述方法来完成配光设计,进而验证该方法的可行性。
3 摩托车信号灯中L ED 制动灯的配光设计与仿真验证
根据《GB478921998 汽车及挂车外部照明和信号装置的安装规定》中规定的摩托车色度条件选取达晟光电的R33CA 型的红光球帽型L ED ,其I0= 4. 55cd ,且θ1/ 2 = 10°。根据《摩托车光信号装置配光性能GB T1751021998》标准,通过球带系数法估算整个灯具所需的总光通量和所需的L ED 的数目,共采用15 个R33CA 型红光L ED 来进行摩托车制动灯的配光设计。
将对应的国标规定的各测点的光强值代入公式(10) 到公式(18) ,通过MA TLAB 求解出方程组的满意解,即采用3 ×5 的排布,γi 为(0 , ±5°, ±10°) ,即每行5 个L ED 采用柱面型排布。
按照方程组的解将建立的15 个L ED 柱面排布的三维模型导入光学仿真软件Tracepro 中,得到的矩形光强分布图如图3 所示,验证其光学效果。
通过方程组(10) —(18) 计算得到国标要求的测点的理论值。从图3 所示的矩形光强分布图中,读取国标要求的测点的仿真值。由于测点关于H2H 对称又关于V2V 对称,则国标要求的测点的光强值可以简化为如表1 所示。
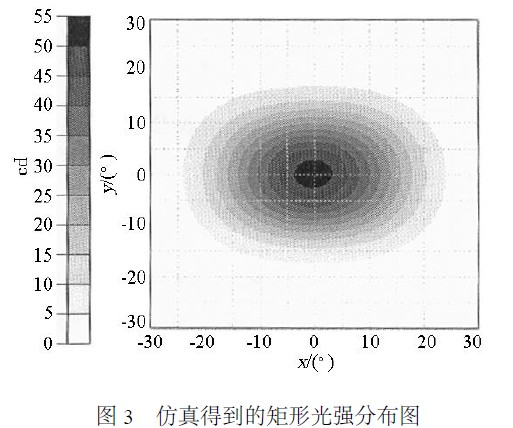
仿真得到的矩形光强分布图
从表1 中的数据可以看出,测试点的光强仿真值都在国家标准要求的范围之内,且仿真值与理论值很接近,而仿真结果也一定误差范围内比较真实的反映了灯具实际的光强分布,从而验证了该设计方案的可行性。
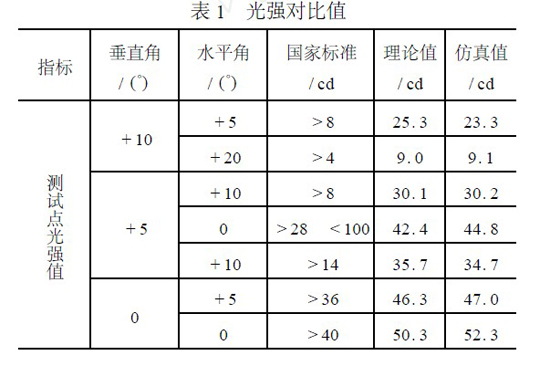
光强对比值
4 结 论
本文提出了一种基于曲面L ED 阵列的光强分布数学模型的新型方法,在推导了曲面L ED 阵列光强分布数学模型的基础上,将其应用于L ED 摩托车信号灯配光设计。进一步采用Tracepro 光学仿真软件对该方法设计的L ED 摩托车制动灯进行了模拟实验,结果证明曲面L ED 阵列光强分布的数学模型正确,能够满足国家摩托车配光标准的要求。该方案设计的L ED 摩托车制动灯光线绝大部分集中在左右20°,上下15°的椭圆形区域内,且无需聚光器和配光镜,光效大大的提高,成本大大的降低,并且生产工艺简单,经济实用。

